Vertex Form

Formula

y = a(x – h)2 + k

Key terms

Vertex
Zereos
intercepts
Optimal value
Axis of symmetry

The formula Above represents the equation

of a given parabola in vertex form. The `y`

stands for the parabola.

The `a` stands for

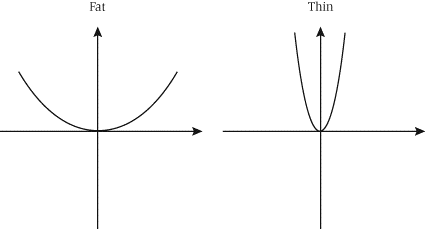
whether the parabola opens upwards or downwards and if its vertically stretched or compressed. We can determine this on two things, if the `a` value is is greater then one, we call it vertically stretched, if it is less then one it is vertically compressed. We can also tell if the parabola is going to open upwards or downwards depending on if the `a` value is negative or positive. For example if the `a` of a given parabola was 0.25 we can figure out that the parabola is going to be facing downwards and is compressed by the factor of 0.25.

The fat is vertically compressed, the thin

is vertically stretched.

`h` value represents

the horizontal shift, so how many units left or right along

the x-axis the vertex is. But the trickey thing is the numbers

are opposite, so if the `h` value is +5 then the parabola is

horzintally shifted 5 units to the left, but if it is -5 then

the parabola is shifted 5 units to the right.

The 'k' value represents

simply stands for how many units the parabola has shifted along the y axis. If the

number is a positive number it has moved upwards along the y-axis and when it is

negative, it has moved down along the y-axis. For example if the equation had a 8 as its 'k' value, you can tell that the parabola for the given equation has moved up 8 units. If it was -8, you would know that the parabola has moven 8 units downwards.

Graphing

When graphing a parabola you need to understand

that the axis of symmetry is the 'h' value in the equation,

and the optimal value is the 'k' value. The axis of

symmetry is the 'x' value of the vertex and the optimal

value is the 'y' value of the vertex. For example if the

equation of the line is y= 2(x-4)2- 3, you would know the

vertex of the parabola would be (4,3). Now to figure out

how the rest of the graph will look like we will now watch

a video on a simple example.

To find points for the graph you must plug in x values to figure out the y values. So if the vertex is (4,3) your next x value would be 5 to figure out the y value, you take the 5 and plug it in. so

y=2(5-4)2-3

y=2(1)-3

y=-1

The next point would be (5,-1) and the same point would be plotted on the other side of the vertex.

For more help on step patterns please feel free to refer to the video above!