Quadratics

Y= a(x-r)(x-s)

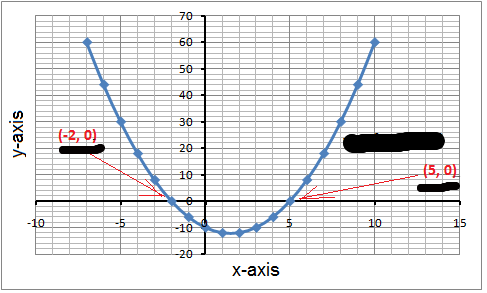
Factored Form is simply breaking down a quadtratic relationship. This equation unlike standard form does not focus on the `b` value of the quadtratic but the `r` and `s`. They both stand for the x intercepts or the zeroes of the equation.

 

 

 

 

 

 

 

 

 

 

 

 

 

To find the vertex of the graph we must first find the axis of symmetry of the parabola.  The axis of symmetry is the half way point between the two zeroes of the parabola and the x value of the vertex. To find this we must add together the zereos of the parabola and divide them by two. To find the zereos of the equation you must make each braket equal 0. Ex;

y=0.5(x-3)(x+4)

 

0=x-3   0= x+4     So the x interecepts of the parabola are 3 and -4.

3=x      -4= x

 

AOS (axis of symmetry) = -4+3/2

                                     = -0.5 

 

Now to find the optimal value we need to insert the AOS into the equation.

The optimal value is the y value of the vertex.

y=0.5(0.5-3)(0.5+4)

y=0.5(-2.5)(4.5)

y=-5.625

 

So the vertex = (-0.5,-5.625)